What are harmonics?

If you can understand them, it gives you a window into how subatomic particles behave

For our last day of pop aural skills class, I did a crash course on historical tuning systems. This involved a brief introduction to harmonics. As I was talking, I realized that my verbal explanation of this concept is still clunky and imprecise. This is a problem, because harmonics are important, not just for music theory, but also for audio engineering, as well as many non-music-related subfields in physics. Including quantum mechanics! 

The easiest way to understand harmonics is to use a guitar. Sit in a quiet place and play the low E string. Don't twang it so hard that it snaps against the fingerboard, just do a solid pluck and let it ring. Listen closely to the sound as it fades to silence. Assuming that the guitar is in standard tuning, you are hearing the note E2, the pitch produced by the guitar vibrating at 82.41 Hertz. This means that the string is completing 82.41 cycles of vibration per second. Simple, right?

Well, no. The string's movement is much more complicated than just wobbling back and forth along its entire length, and its vibration produces more pitches than just E2. If you listen carefully, you can hear these other pitches. You have been hearing them in many musical sounds for your entire life, whether or not you were conscious of it. Let's focus in deeper on the sound of the guitar string and see if we can understand it better.

The very first thing you hear when you pluck a guitar string is a short, sharp burst of noise, that is, many frequencies blended chaotically together. This burst of noise is called a transient. If you were banging on a miscellaneous metal object, the transient (a plunk or clunk) is probably all you would hear. If you bang on a more flexible piece of metal, it might resonate, and that resonance might have a distinct pitch to it. There are a couple of metal mixing bowls in my kitchen that make perfect bells or gongs if you tap them in the right place.

Guitar strings are not ordinary metal objects. They are designed to vibrate easily, and the guitar is designed to maximize the strings' resonance. When you pluck, you send waves of displacement cascading down the string to its ends. The waves then bounce off the string's ends, racing back and forth, mixing together, and interfering with each other and themselves. This interference quickly self-organizes into standing waves. The animation below shows a simplified version of the process. 

The green wave is traveling to the right, and the blue wave is traveling to the left. They interfere with each other to produce the red wave. When the peaks of the green and blue waves line up, the red wave reaches its maximum displacement. Where the green and blue waves cancel each other out, the red wave doesn't move at all. These cancelation points are called nodes. The red dot in the center of the image is a node. This will be important later.

The guitar string produces standing waves at each of its resonant frequencies. The largest-amplitude resonance is the string's first harmonic, otherwise known as its fundamental frequency. The low E string's fundamental frequency is 82.41 Hz, and it produces the pitch E2. We conventionally describe this pitch as "the note" produced by the string. However, while E2 is the string's loudest audible resonance, it is far from the only one. These frequencies have a surprisingly simple mathematical relationship: they are all whole-number multiples of the fundamental.

Listen as the note decays and you will hear the sound change. As the fundamental fades out, you can hear a higher E still ringing. It was always there, but the fundamental masked it at first. The higher E is the string's second harmonic, a vibration at 164.81 Hz, twice as fast as the fundamental. The second harmonic produces the note E3, an octave higher than E2. This two-to-one frequency ratio is the definition of an octave. (If it's a factor of two, why is the word "octave" derived from the number eight? Don't worry about it for now.)

Keep listening to the sound of the string as it decays, and you should be able to hear the third harmonic emerging out of the sound as the first and second harmonics fade out. The third harmonic is a vibration at 247.22 Hz, three times faster than the fundamental. It produces the pitch B3, a fifth plus an octave higher than E2. This is the same pitch produced by the open B string. In fact, the B string has probably been resonating sympathetically along with the E string this whole time.

The next higher (and quieter) sound to listen for is the fourth harmonic, a vibration at 329.63 Hz, four times as fast as the fundamental. The fourth harmonic produces E4, two octaves higher than E2. This is the same pitch produced by the open high E string. Like the B string, the high E string likes to resonate sympathetically with the low E string. These mutually reinforcing resonances are what make open E and Em chords sound so good on the guitar.

If you really focus deeply, you may be able to detect the fifth harmonic, a 412.04 Hz vibration, five times faster than the fundamental. It produces G#4, a major third plus two octaves higher than E2. Hearing the fifth harmonic on an acoustic guitar takes practice, but you might have an easier time hearing it on an electric guitar that is heavily distorted or feeding back.  

There are even more audible harmonics of the low E string, though you are unlikely to be able to pick them out just by listening: the sixth harmonic at 494.44 Hz, producing the pitch B4; the seventh harmonic at 576.87 Hz, producing a very flat D5; the eighth harmonic at 659.28 Hz, producing E5; the ninth harmonic at 741.69 Hz, producing F#5; the tenth harmonic at 824.07 Hz, producing G#5; and the eleventh harmonic at 906.48 Hz, producing a wildly flat A#5. Notice that as the harmonics get higher, their pitches get closer together. You are probably not conscious of any of these higher harmonics, but they affect your experience of the guitar's timbre, and the sound would be dull and colorless without them.

The specific loudnesses of the guitar string's harmonics and their different rates of decay depend on a lot of factors: the instrument's construction, the makeup of the string and its age, how hard you pluck, where on the string you pluck, whether you are using a pick or your fingers, the angle of the pick or your fingers, and so on. This is a lot of physical parameters, and they result in a highly complex sound! You can see why it's so difficult to synthesize the guitar believably.

You may not be able to hear harmonics when they are blended together in the sound of a plucked string, but the good news is that you can isolate them so you can hear them by themselves. All you have to do is lightly touch the vibrating string at one of the harmonics' nodes. (Remember those?) This lets your harmonic of choice keep ringing, while deadening all of the other harmonics that normally obscure it.

• To isolate the second harmonic, touch the string at its halfway point, which is at the twelfth fret. (This means right above the fret itself, not the place where you would normally finger the string.)

• To isolate the third harmonic, touch the string a third of the way along its length, at the seventh fret.

• To isolate the fourth harmonic, touch the string a quarter of the way along its length, at the fifth fret.

• To isolate the fifth harmonic, touch the string a fifth of the way along its length, between the third and fourth frets. This spot will take some trial and error to find.

In this video, Miles Okazaki demonstrates how to isolate the first seven harmonics of the guitar strings.

It is more challenging to find harmonics beyond the fifth one. I can reliably find the first eleven, but only after hunting around for a while. Apparently, higher harmonics are easier to isolate on brass instruments. Martin Lawrence from the Orchestra of the Age of Enlightenment demonstrates the first thirteen harmonics of the horn.

Martin Lawrence has strong negative emotions about the eleventh and thirteenth harmonics. It is true that the intervals they produce have not historically been part of Western Europe's musical vocabulary. But the seventh harmonic hasn't either. It is much flatter than the flat sevenths that are part of standard Western tuning. You do hear harmonic sevenths in the blues and related styles, though.

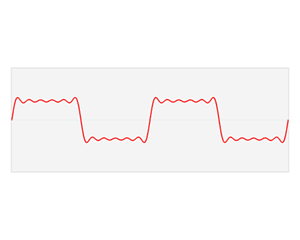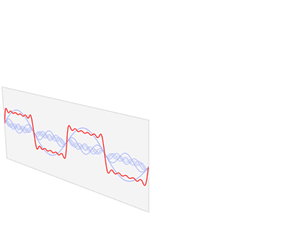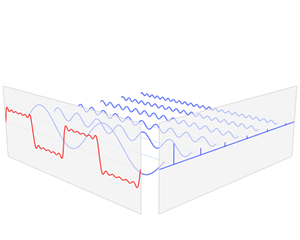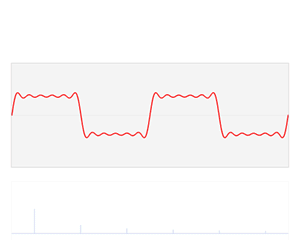
How do individual string harmonics combine to make the rich and complex timbre of the guitar? This is one of those physics questions where intuition is not much help, and you really need to approach it mathematically. The concept you need is called the Fourier transform, named for the French mathematician Jean-Baptiste Joseph Fourier. Fourier's insight was that you can represent any repeating waveform (like a guitar string's vibrations) by adding together simple sine waves (the harmonics). The animation below shows how you can add sine waves together to make a square(-ish) wave. Guitars don't produce square waves, but oboes (sort of) do.

The Fourier transform made more sense to me when I learned to understand sine waves as the curve being swept out by a clock hand going around in a circle, as in these animations: 

These clock hands are called phasors. You can experiment with summing phasors together using this beautiful interactive visualization by Jack Schaedler. Understanding phasors is not necessary for playing the guitar, but they are a window into a wide range of physical systems, including... subatomic particles!

If you read this blog for music content and don't want to deal with quantum mechanics, you should stop reading here. You should also stop reading if you want to learn about quantum mechanics from an actual scientist. But if you want to see a music teacher try to convey his own limited and partial understanding of quantum mechanics, read on. If you are a real scientist and you see something wrong here, please correct me!

The hardest thing to understand about subatomic particles is that they are not little marbles. All those pictures in your science textbook were wrong! Particles behave like little marbles in some situations, but that is not what they fundamentally are. You can get a better understanding from TV static. Each little dot in the static is an electron hitting the screen. Now imagine that the screen is empty space, and the dots are electrons flickering in and out of existence. The likelihood of the electron flickering into existence at a certain spot depends on the strength of the electron field at that spot. 

Here is where harmonics come in. When an electron is part of an atom, it doesn't just jump around randomly like in TV static. Well, it does jump around kind of randomly, but there is a specific organizational scheme to the places where it is likeliest to pop up. These organized spaces are called orbitals, and they are to the electron field what harmonics are to guitar strings. The electron field has waves, and those waves undergo interference, producing standing waves that are the three-dimensional equivalent of the guitar string's one-dimensional harmonics.

Now comes the part that I have trouble verbalizing. Electron waves have to be a whole number of wavelengths long, for the same reason that guitar string resonances can divide the string by two or three or four, but not by two and a half or three and a quarter. You can have a second harmonic or a third harmonic, but not a second-and-a-half harmonic. They only come in discrete units of one. Electron waves work the same way. That discreteness is the "quantum" part of quantum mechanics.

If, like me, you were brought up to imagine particles as being little marbles, it's very difficult to imagine them as waves. This is where music education can be helpful for science education. Albert Einstein drew an explicit connection between acoustic waves and atomic orbitals. In 1940, he wrote that atoms can have only discrete energy values because they behave like the harmonics of organ pipes or strings. He was an enthusiastic amateur violinist and certainly experienced string harmonics. I don't know whether his violin playing was the basis for his broader understanding of harmonic oscillators or whether they complemented each other, but I do know that the concept of electron orbitals made zero sense to me until I made the connection to string harmonics.