The harmonic family tree
My blog stats have made it crystal clear that very few of you want to read about tuning systems. However, a vocal minority of you do love reading about them, and I definitely enjoy writing about them. So, let's dig in and see how much Western harmony we can derive from the natural overtone series!
Imagine that you are building a guitar. You start by putting on a string tuned to a note called C3. When you pluck your C string, it vibrates at a frequency of 1 Hz, meaning that it vibrates back and forth once per second. (In real life, a guitar string tuned to C3 would vibrate back and forth at 130.8128 Hz, so multiply all the numbers in this post by 130.8128 if you want to think in terms of actual frequencies.)
The string doesn't just vibrate along its entire length. Subsections of the string also vibrate independently. These subsection vibrations are called harmonics. Each harmonic produces its own distinct pitch. When you pluck a string, you are hearing a lot of pitches from the complex blend of all of the harmonics. This means that every note you play on the guitar is really a chord!
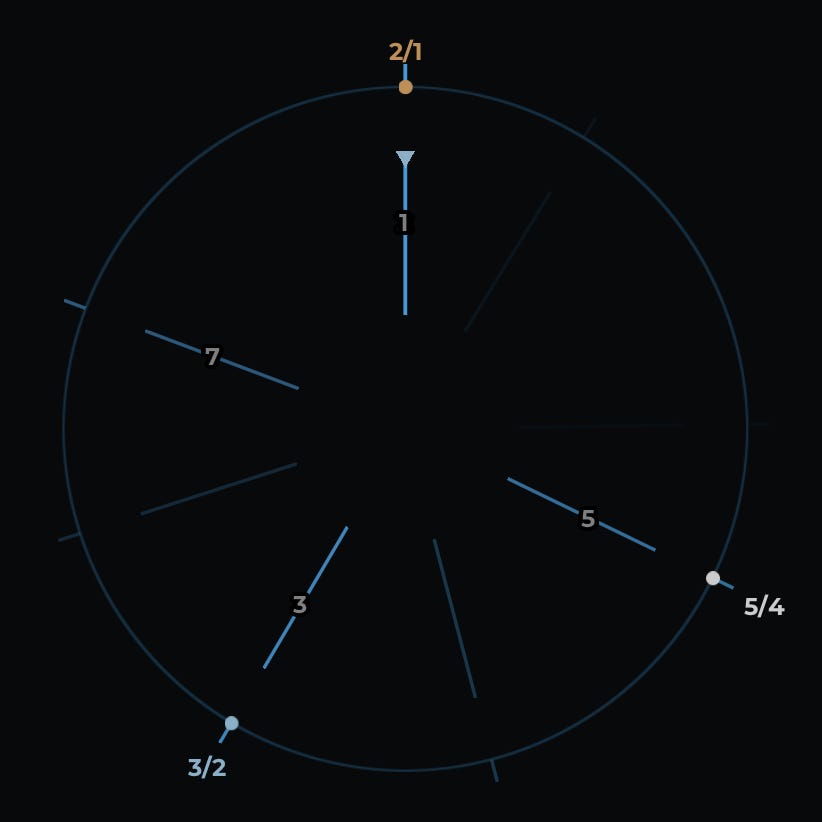
Here is an animation of the first four harmonics of a string.
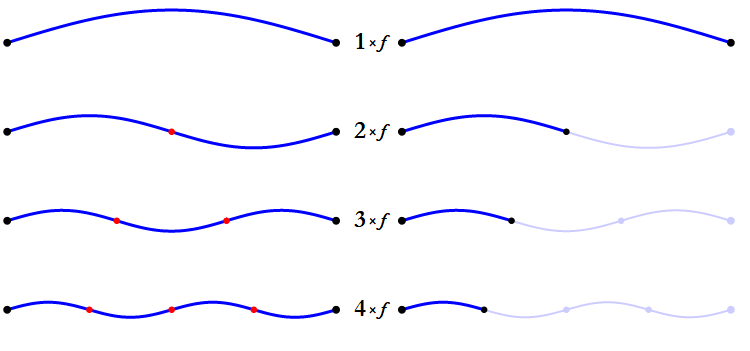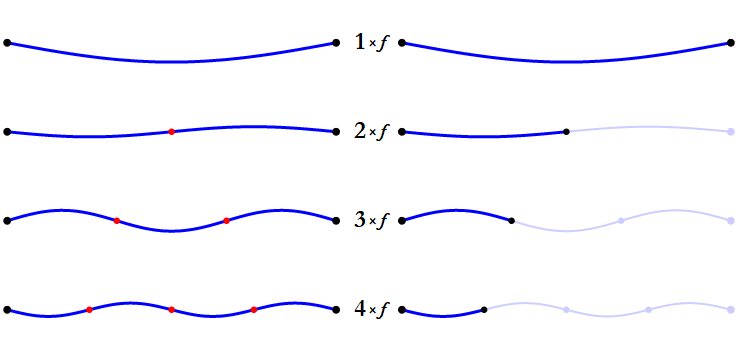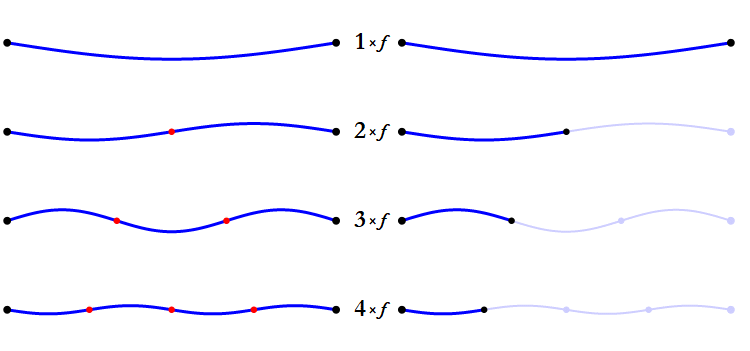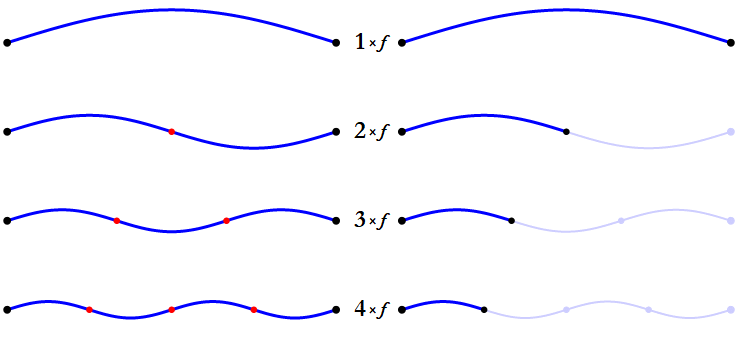
The first harmonic of a guitar string is its vibration along its entire length (also known as the string's fundamental.) The second harmonic is the string's vibration in halves. Each half vibrates twice as fast as the whole string, so it produces a higher pitch than the first harmonic does. Specifically, the pitch of the second harmonic is one octave higher than the pitch of the first harmonic. If the string is tuned to C3, then its second harmonic will produce C4. But they are totally different pitches! Why on earth are they both named C?
To understand why we consider octaves to be equivalent, imagine adding a second string to the guitar that's half as long as the first one. This new string will play C4. We'll call it the high C string, and we'll call our original string the low C string. If you strum both C strings, their harmonics will overlap extensively.
The high C string's first harmonic will be the same as the low C string's second harmonic.
The high C string's second harmonic will be the same as the low C string's fourth harmonic.
The high C string's third harmonic will be the same as the low C string's sixth harmonic.
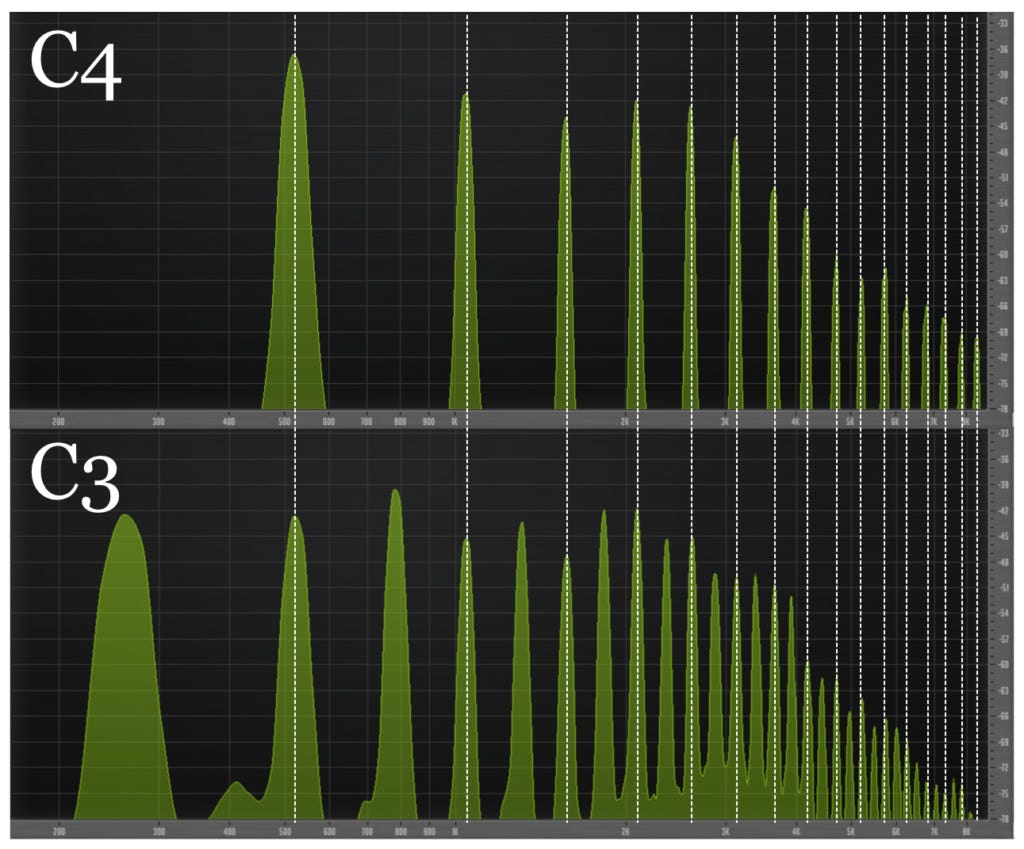
Your ear will have no trouble detecting the overlap between the two strings' harmonic series. This spectacular agreement is the reason why Western music theory considers C3 and C4 to be "the same" note (technically, the same pitch class.) The important concept here is that because octaves are equivalent, you can double or halve the fundamental frequency of any note and it will remain the "same". This will be important later.
Anyway, let's go back to the harmonic series of the original C string.
The string's third harmonic is its vibration in thirds. Each third vibrates three times as fast as the whole string, producing a new note called G.
The string's fourth harmonic is the vibration in quarters. Each quarter vibrates four times as fast as the whole string, producing yet another C. (Even-numbered harmonics are boring because they always produce higher-octave copies of the pitches produced by odd-numbered harmonics.)
The string's fifth harmonic is its vibration in fifths. Each fifth vibrates five times as fast as the whole string, producing a new note called E.
Here's a schematic diagram of the notes you get from the first five harmonics of the C string. The third harmonic, G, has a frequency of 3 Hz. The fifth harmonic, E, has a frequency of 5 Hz.
The next thing we're going to do is to add two new strings to the guitar. One will be tuned to G, and the other will be tuned to E. It will sound better if we move the G down an octave to 3/2 Hz, and the E down two octaves to 5/4 Hz.
Strumming the C, G and E strings makes a lovely chord called C major. Why does it sound so good? For one thing, the G string's second, fourth, sixth and eighth harmonics produce the same pitches as the C string's third, sixth, ninth and twelfth harmonics.
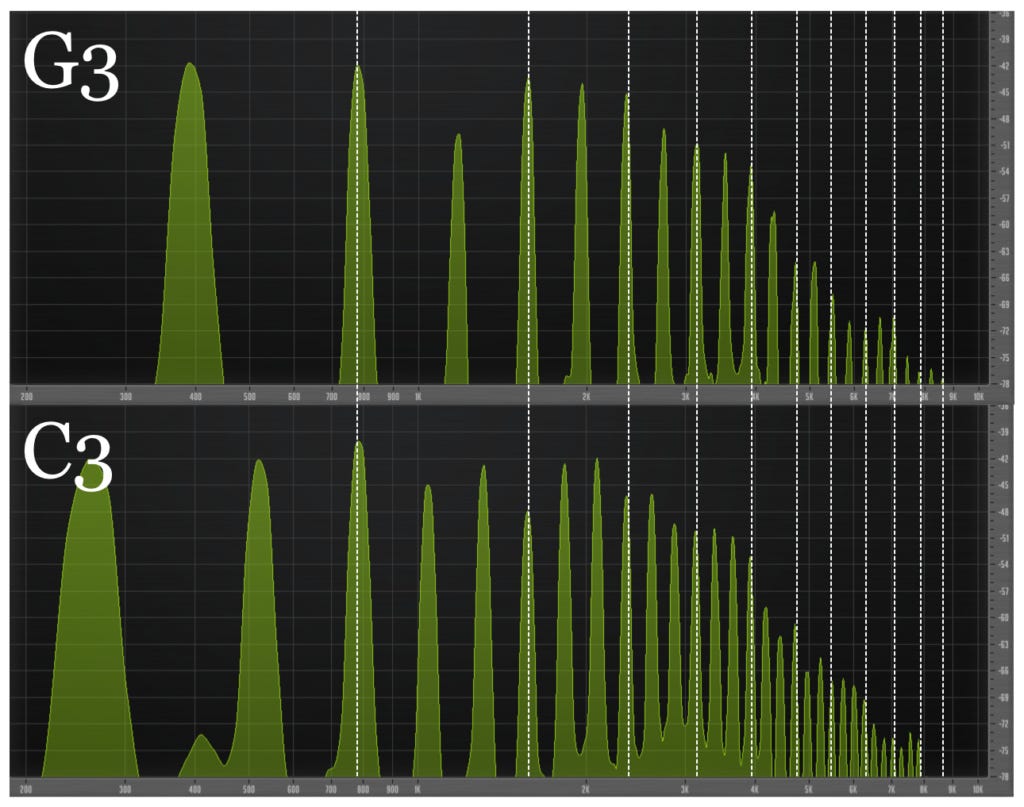
For another thing, the E string's fourth, eighth, twelfth and sixteenth harmonics produce the same pitches as the C string's fifth, tenth, fifteenth and twentieth harmonics.
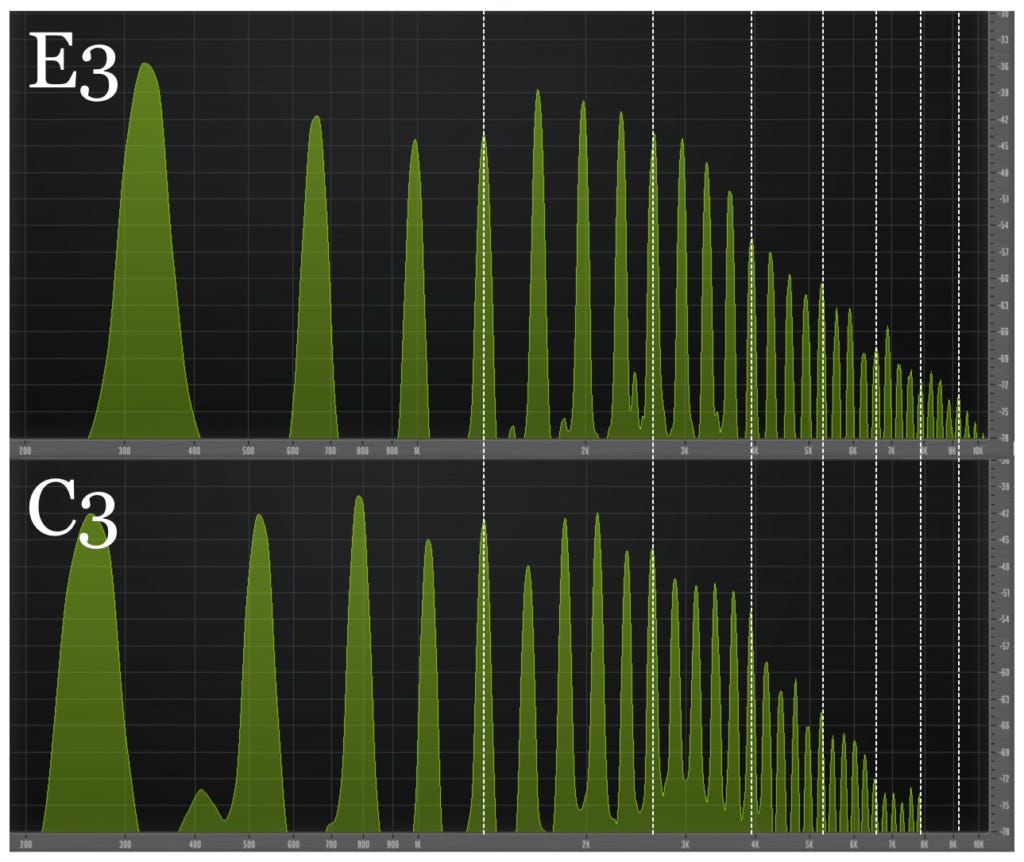
And for yet another thing, the G string's fifth, tenth, fifteenth and twentieth harmonics produce the same pitches as the E string's sixth, twelfth, eighteenth and twenty-fourth harmonics.
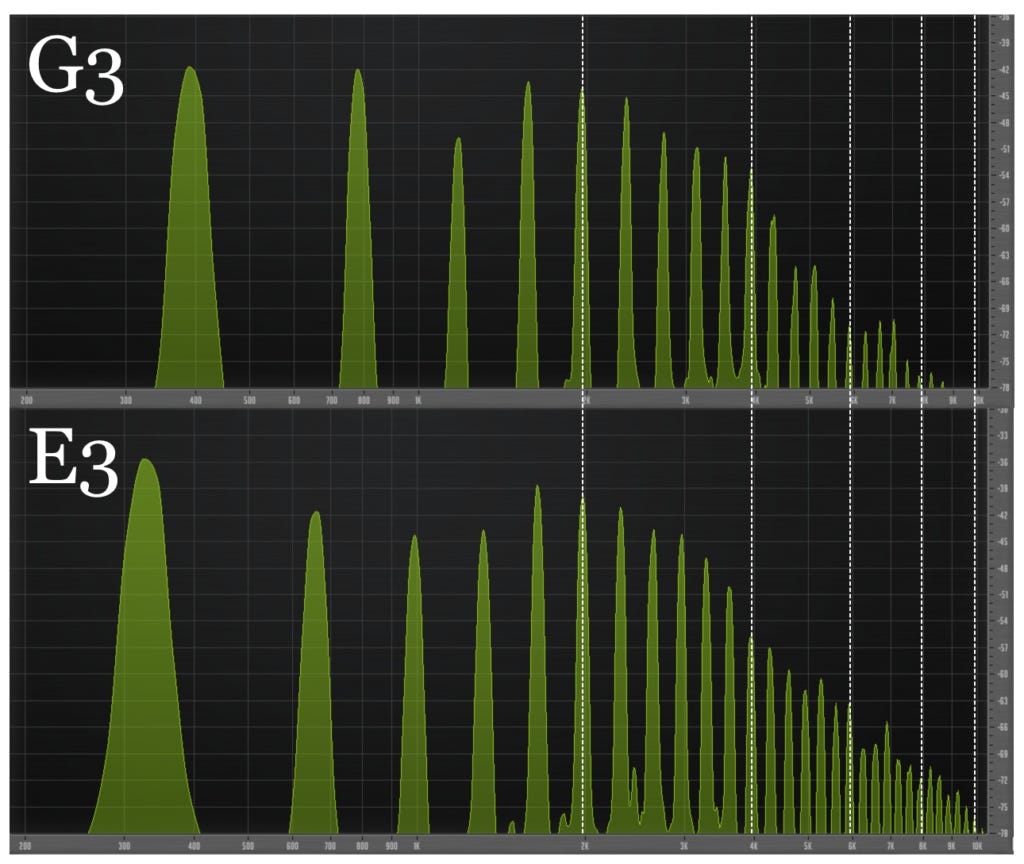
That is extraordinary alignment! Your ear hears all these harmonics dovetailing together and thinks, this can't be a coincidence, it must mean something.
https://www.youtube.com/watch?v=UQG5rsCtU2M
We can find more related notes by examining the first five harmonics of the G and E strings.
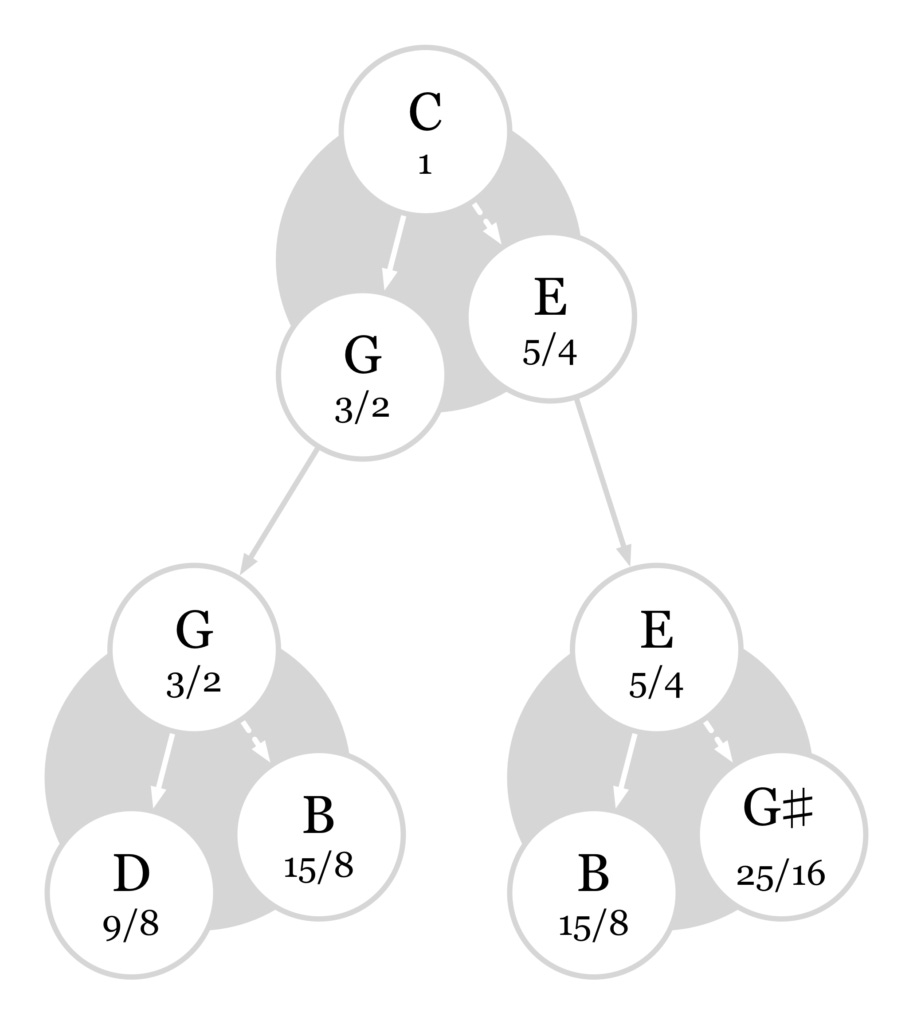
The G string's third harmonic produces the note D, and its fifth harmonic produces the note B. The E string's third harmonic produces that same B, and its fifth harmonic produces G-sharp. Let's add three more strings to the guitar, tuned to D, B, and G-sharp.
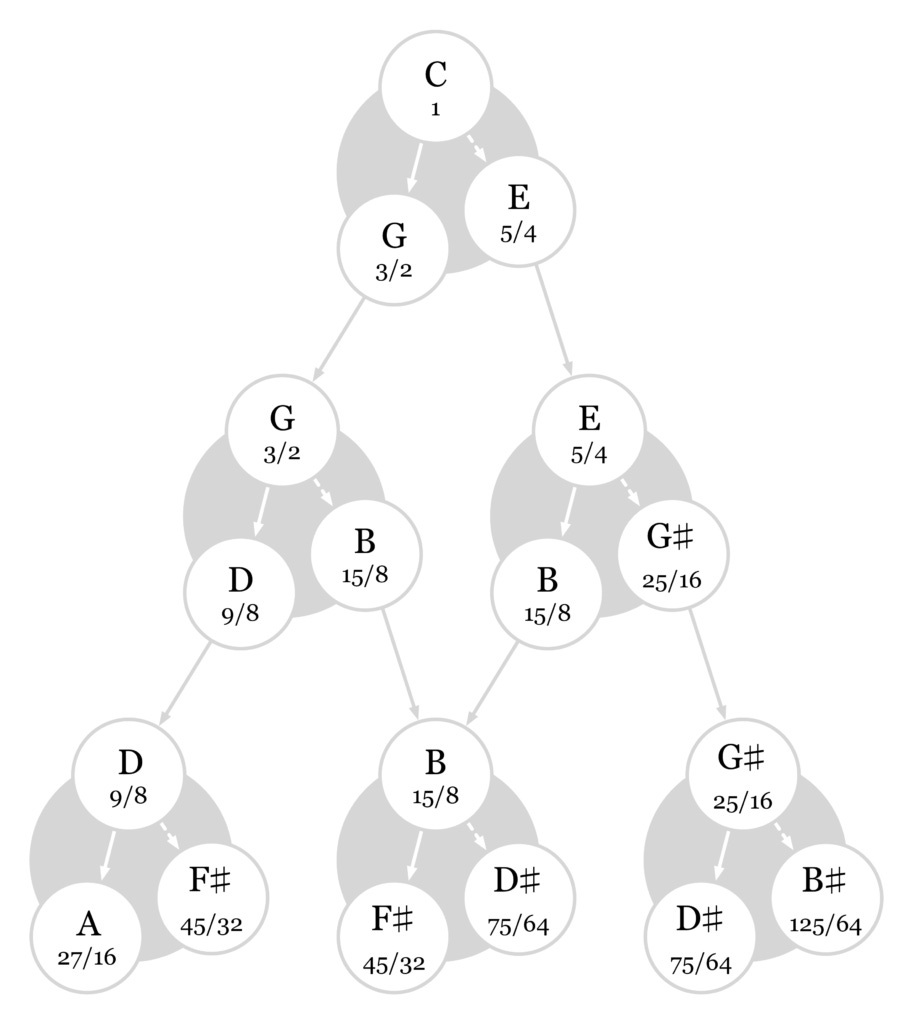
The D string's third harmonic produces A, and its fifth harmonic produces F-sharp. The B string's third harmonic produces F-sharp, and its fifth harmonic produces D-sharp. The G-sharp string's third harmonic produces D-sharp, and its fifth harmonic produces, uh, B-sharp. That last note is an oddball. Pianos don't have B-sharp! This note is only 3/64 Hz flatter than C. Weird.
Anyway, now let's use a new strategy to find more notes. We will move up the family tree rather than down it. In other words, rather than looking at the harmonics of C, we are going to identify notes whose own harmonic series include C. If we add an F string, its third harmonic will produce C. If we add an A-flat string, its fifth harmonic will produce C.
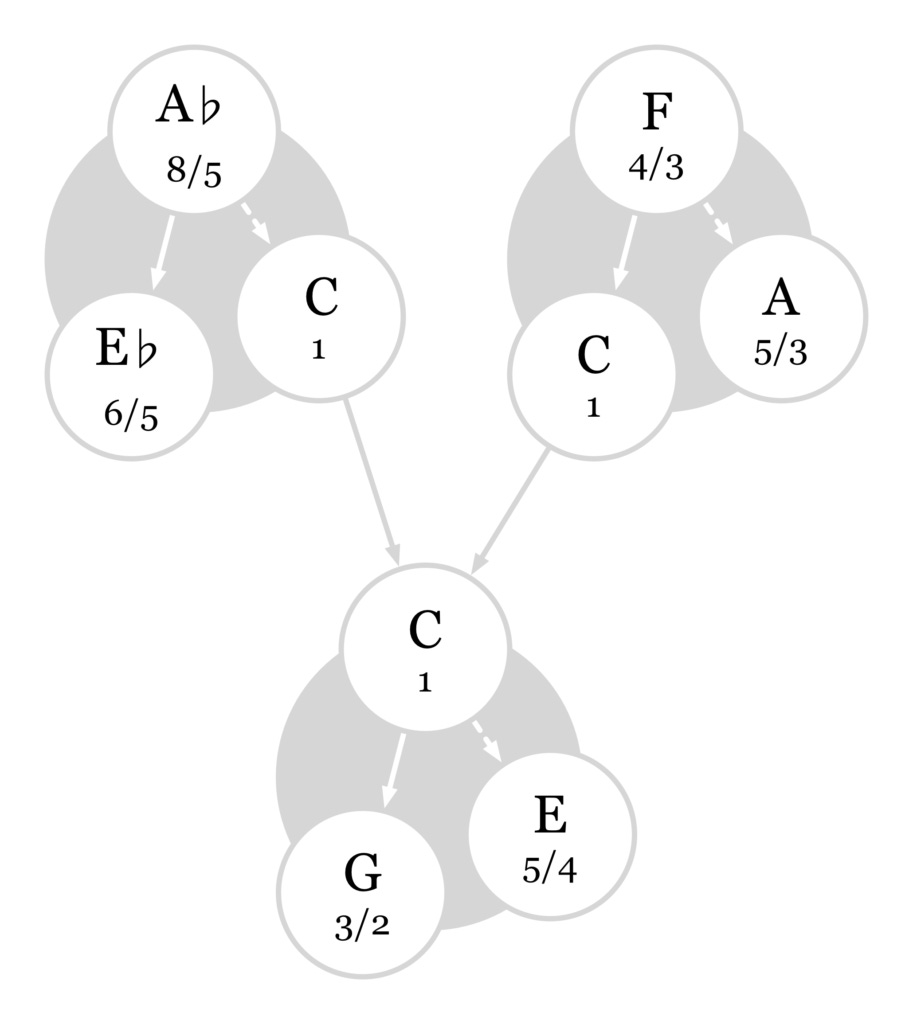
The A-flat and F strings also have some new notes in their harmonic series, E-flat and A. Notice that E-flat is not quite the same pitch as D-sharp. They are not interchangeable with each other!
E-flat is interesting for another reason too. When you combine it with C and G, you get a C minor chord. E-flat's fifth harmonic is the same as C's sixth harmonic and G's fourth harmonic. (C and E-flat have the same relationship as E and G, pictured above.) That is not as dense an overlap as C major, but it's still a lot of alignment. Again, Richard Dreyfuss says it best:
https://www.youtube.com/watch?v=UQG5rsCtU2M
Let's keep working backwards up the family tree and figure out the harmonic "parents" of A-flat and F. That gives us three new strings tuned to F-flat, D-flat, and B-flat.
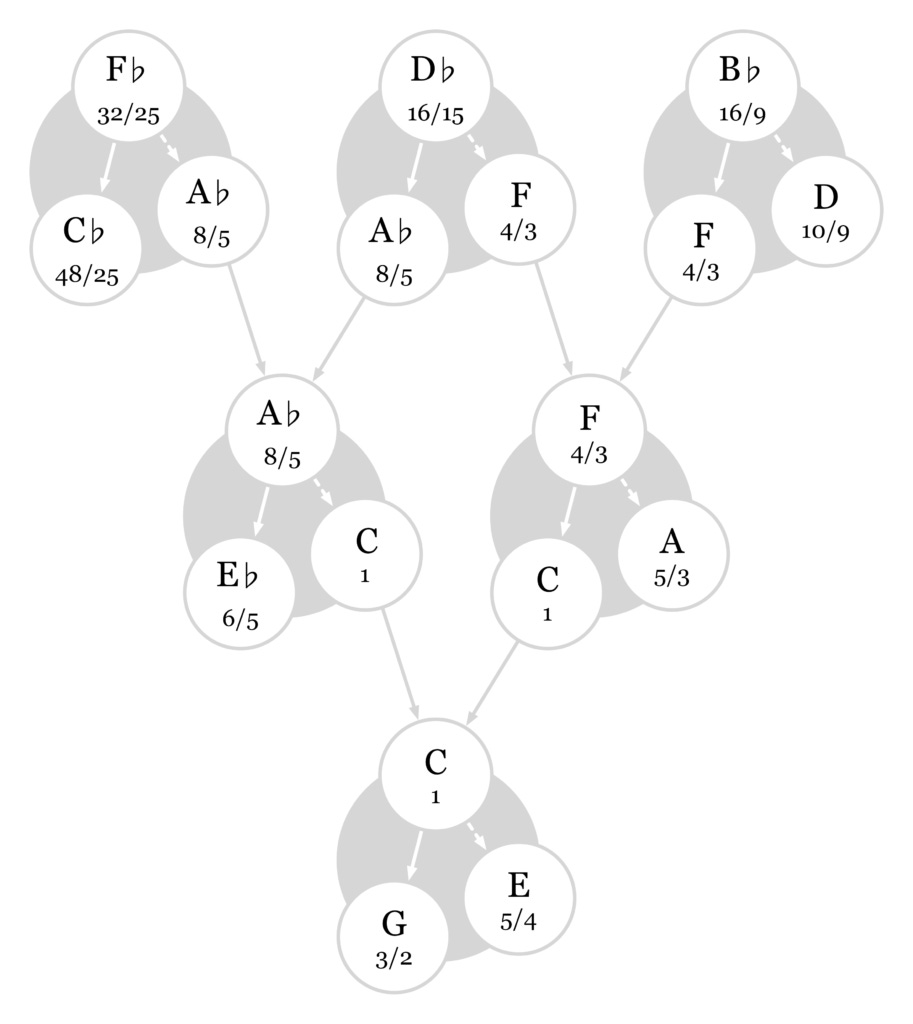
F-flat is another weird and unfamiliar note. It's not quite the same pitch as E. You can't play F-flat on the piano.
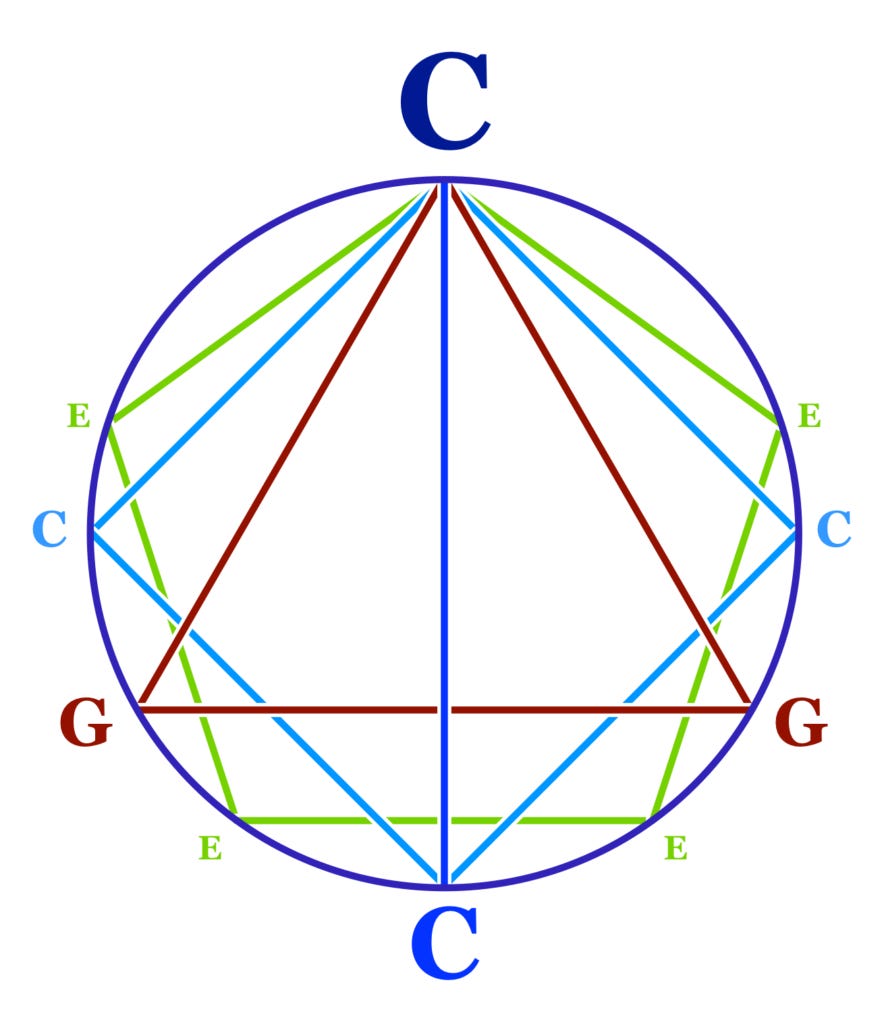
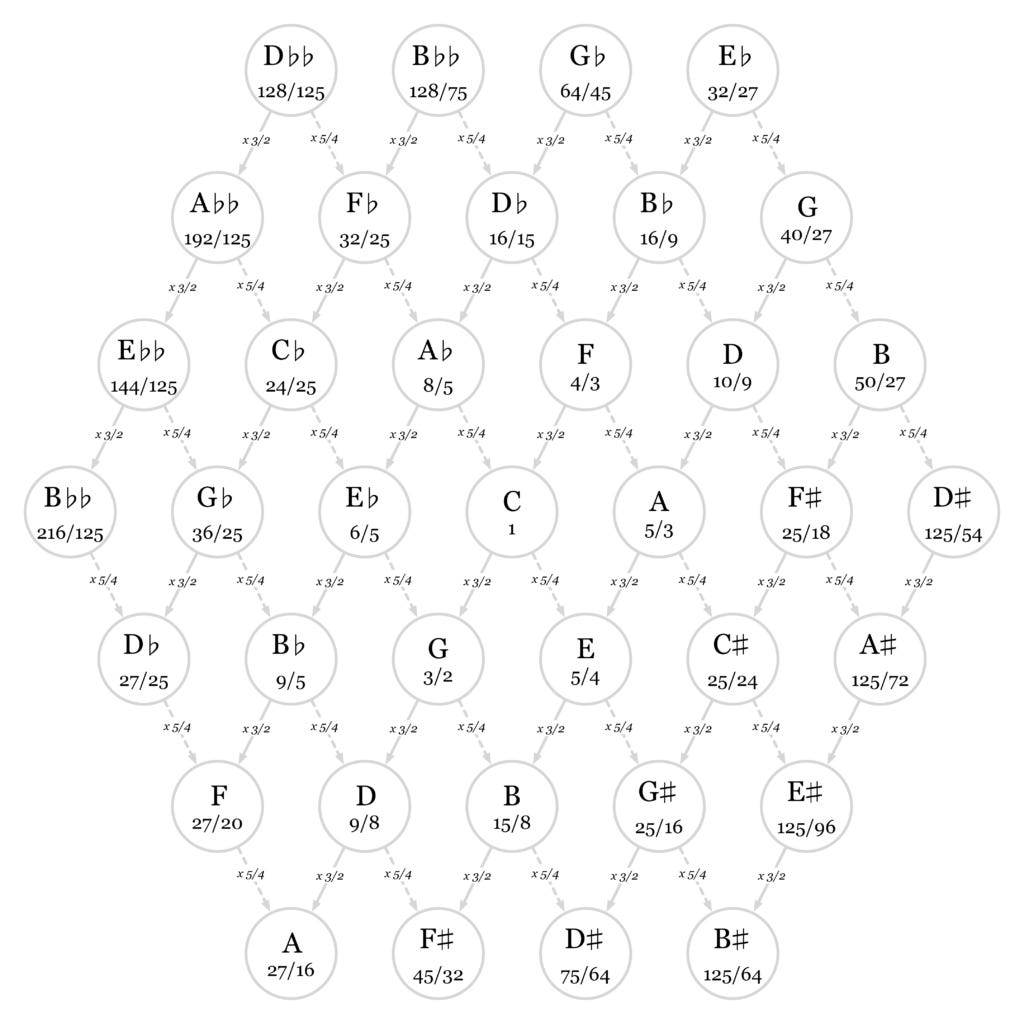
It's possible to keep expanding this harmonic family tree infinitely in all directions. Here are C's eighteen closest relatives.
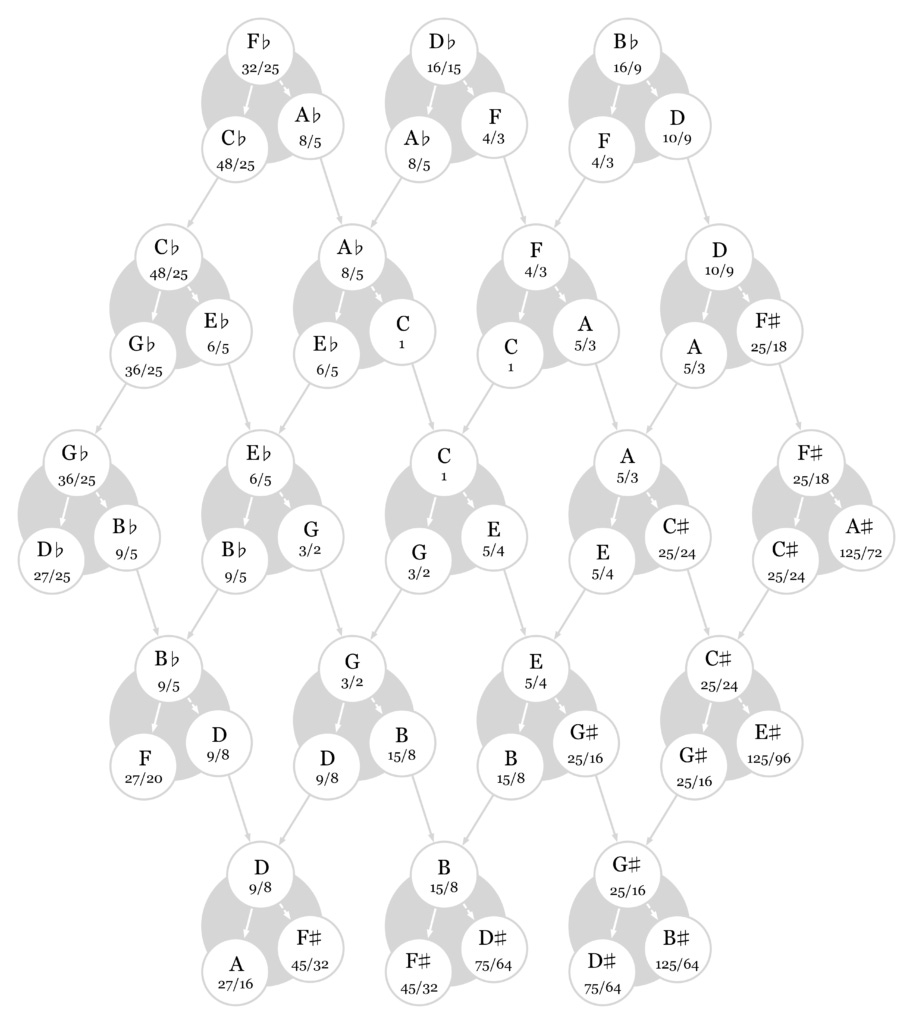
Here's a visually simplified version:
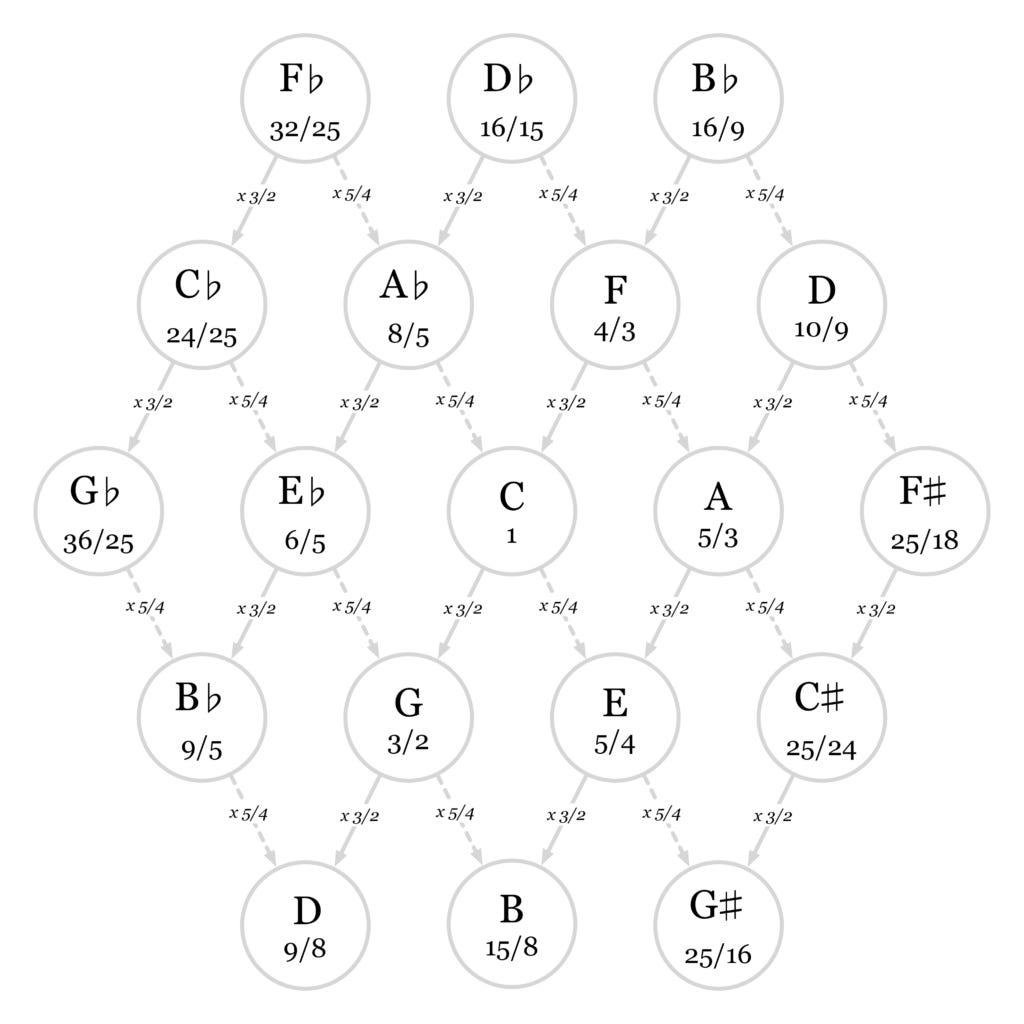
This diagram is called a tonnetz, and it is rich in musical structure. Every group of three contiguous notes is a chord! The triangles that point upwards are major triads, and the triangles that point downwards are minor triads. You can make great chord progressions just by moving around the tonnetz via adjoining triangles.
Hear parts of the family tree thanks to the magic of MTS-ESP:
<a href="https://ethanhein.bandcamp.com/album/music-theory-songs">Music Theory Songs by Ethan Hein</a>
In this track, you are hearing C's descendants via 3rd harmonics, then C's descendants via 5th harmonics, then C's ancestors via 3rd harmonics, and finally C's ancestors via 5th harmonics. Here's a condensed score. (The tuning sounds different from my track, because Noteflight uses twelve-tone equal temperament. More on that below.)
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>
If you examine the family tree diagram closely, you will notice that it has some contradictions in it.
There is a "grandchild" D at 9/8 Hz, but also an "uncle" D at 10/9 Hz.
There is a "sibling" A at 5/3 Hz, but also a "great-grandchild" A at 27/16 Hz.
There is a "nephew" B-flat at 9/5 Hz, but also a "grandfather" B-flat at 16/9 Hz.
What do we do? We could decide to run with the grandchild D, but then it will clash with the uncle's closest relatives. If we use the uncle D, then it will clash with the grandchild's closest relatives.
It gets worse. If we expand the family tree further, it produces more conflicts.
One solution to the problem of conflicting notes would be to use fewer harmonics. Throughout this post, I have been describing a tuning system called five-limit just intonation, because it uses harmonics one through five. Medieval Europeans used a simpler system called three-limit just intonation, which only used harmonics one through three. In three-limit, you start with some note, then generate a new note from its third harmonic, then generate a new note from that note's third harmonic, and so on. Here's a diagram of three-limit just intonation, arranged in a handy configuration called the circle of fifths. (Except that in just intonation, it isn't a circle, it's a spiral.)
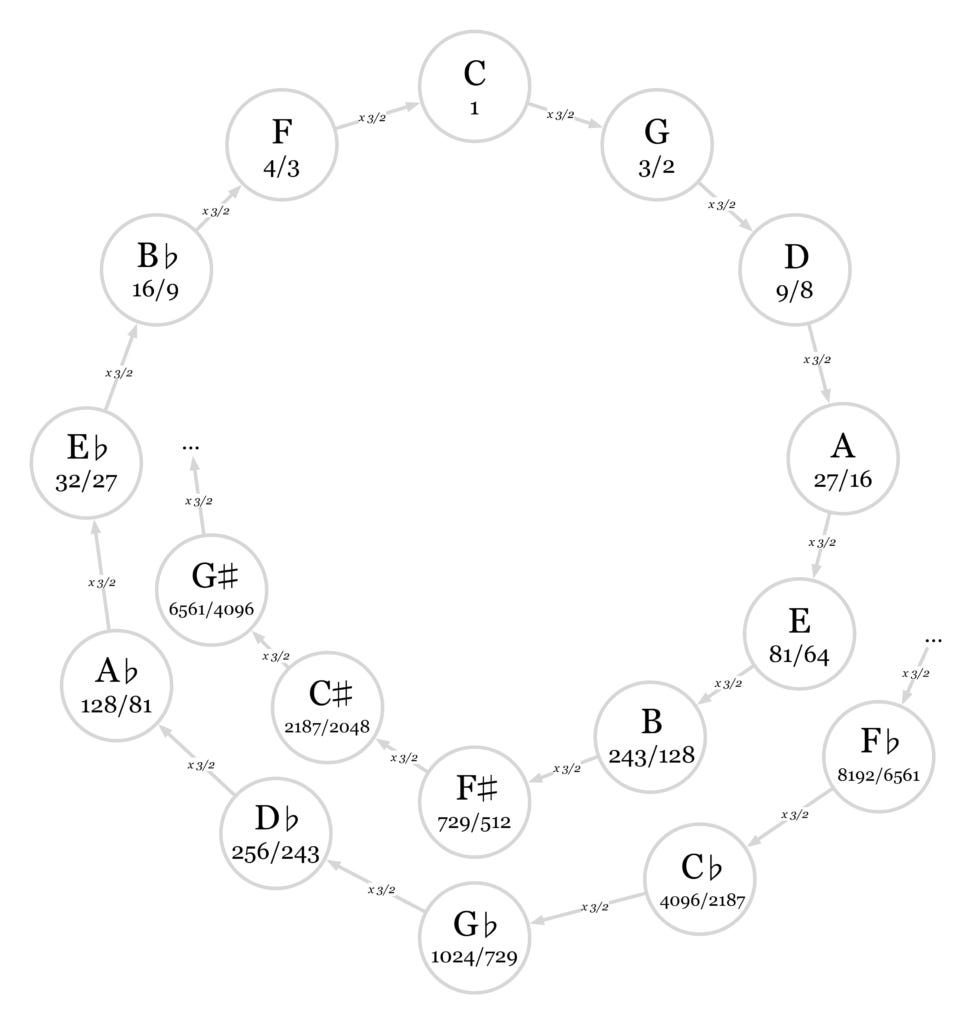
Three-limit just intonation has no conflicts. There is only one D, there is only one A, there is only one B-flat, and so on. Every note has one and only one tuning. C-sharp and D-flat are still different notes, but that's okay, you can work around that. So, great! Why bother with five-limit at all? The problem is that three-limit produces terrible-sounding thirds.
Remember that your ear wants notes to line up with each others' harmonic series. Your ear likes hearing the E at 5/4 Hz together with the C at 1 Hz because E's fourth harmonic is the same as C's fifth harmonic. However, in three-limit, E is tuned to 81/64 Hz. That note's harmonics won't line up with the low harmonics of C at all; it's way too sharp. E-flat is similarly problematic. Your ear likes the five-limit E-flat at 6/5 Hz because its fifth harmonic is the same as C's sixth harmonic. In three-limit, however, E-flat is 32/27 Hz, and that is too flat to have any good harmonic overlap with C. The three-limit versions of A and A-flat are similarly bad-sounding. No wonder medieval Europeans considered thirds and sixths to be dissonant. In three limit, they are dissonant.
What if you go higher in the harmonic series instead? The sixth harmonic is boring, it just produces a higher-octave G. The seventh harmonic is interesting, however: it gives you a B-flat at 7 Hz. That is much flatter than the three-limit B-flat at 16/9 Hz or the five-limit B-flat at 9/5. I put a downward arrow next to it to indicate that it's a different note.
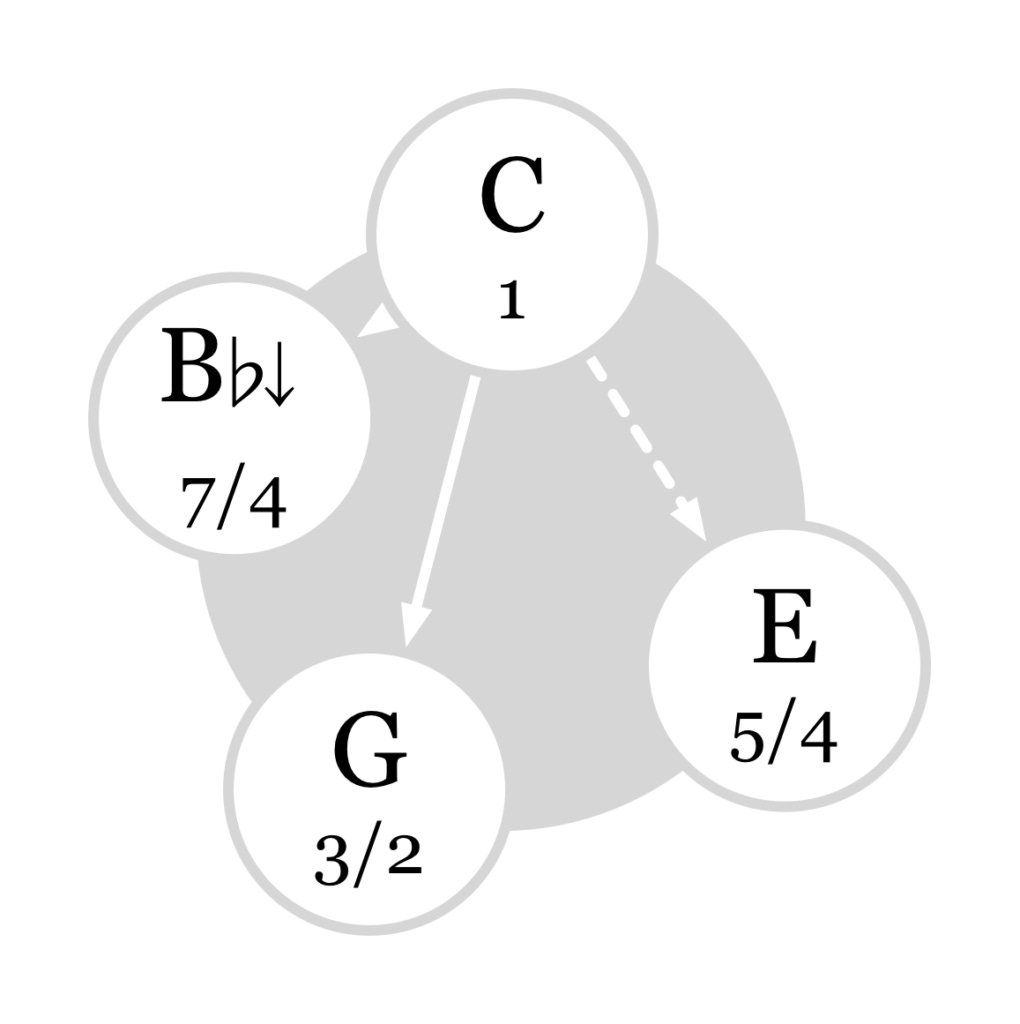
Harmonic sevenths give you beautifully consonant seventh chords. A C7 chord with a harmonic seventh in it feels stable and resolved. This sound is a likely basis for blues tonality.
However, putting the seventh harmonic into the mix makes the family tree extremely complicated. In addition to the conflicting values of the three-limit and five-limit versions of notes, you also get even more conflicts from the seven-limit versions. The diagram below shows just a small part of the seven-limit harmonic family tree.
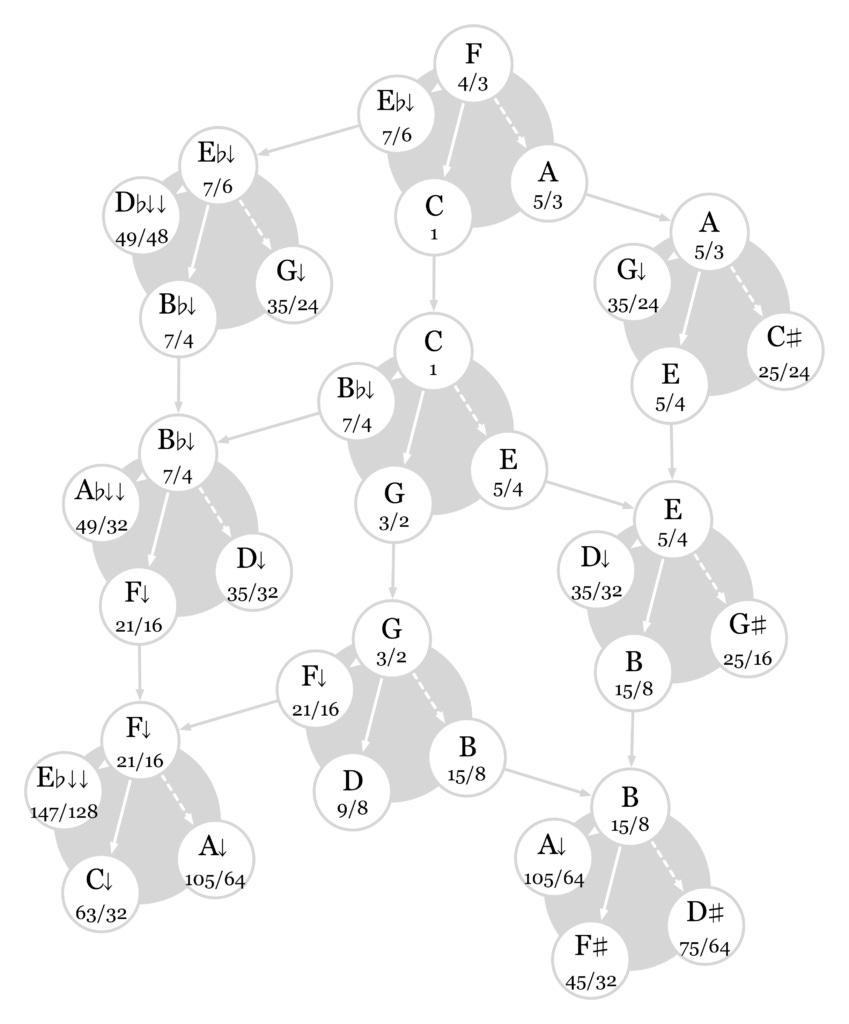
In the blues, this complexity is not such a problem, because you rarely venture far from the tonic anyway. If you are playing the blues in C, you only need to use the seven-limit harmonics of C and F, and maybe G. That is plenty of fine subdivisions of the octave already. But Western Europeans like to jump around among the keys, and that requires a smaller and more standardized set of pitches to work from.
There is another reason to want to have a smaller collection of pitches. I have been blithely talking about adding strings to the imaginary guitar, but real instruments have limits. You only want to have so many strings, so many frets, so many keys on the keyboard. Designing a keyboard or fretted instrument for just intonation is very difficult, because you need a lot of keys or frets to play notes that are very close to each other. Remember that in five-limit, C-sharp and D-flat are two slightly different pitches, as are D-sharp and E-flat, E and F-flat, F-sharp and G-flat, G-sharp and A-flat, A-sharp and B-flat, B and C-flat, and B-sharp and C. Some historical keyboard makers did try making instruments with split black keys and multiple manuals that could distinguish between, say, F-sharp and G-flat, but they were too complicated to catch on. Imagine tuning one of those things!
https://www.youtube.com/watch?v=17HHXS-Jjbg
Western Europeans tried making all kinds of tweaks and adjustments to five-limit just intonation to resolve its many conflicts and awkwardnesses. The eventual consensus solution was twelve-tone equal temperament (12-TET), the system we all use today. In 12-TET, you don't use harmonics to derive your notes. Instead, you build intervals out of uniformly sized semitones. To go up a semitone from any note, you multiply its frequency by the twelfth root of two. To go down a semitone from any note, you divide its frequency by the twelfth root of two. This gives an approximation of just intonation intervals, while also limiting the possible pitches to only twelve per octave. When you play piano or guitar, the adjacent keys and frets play 12-TET semitones.
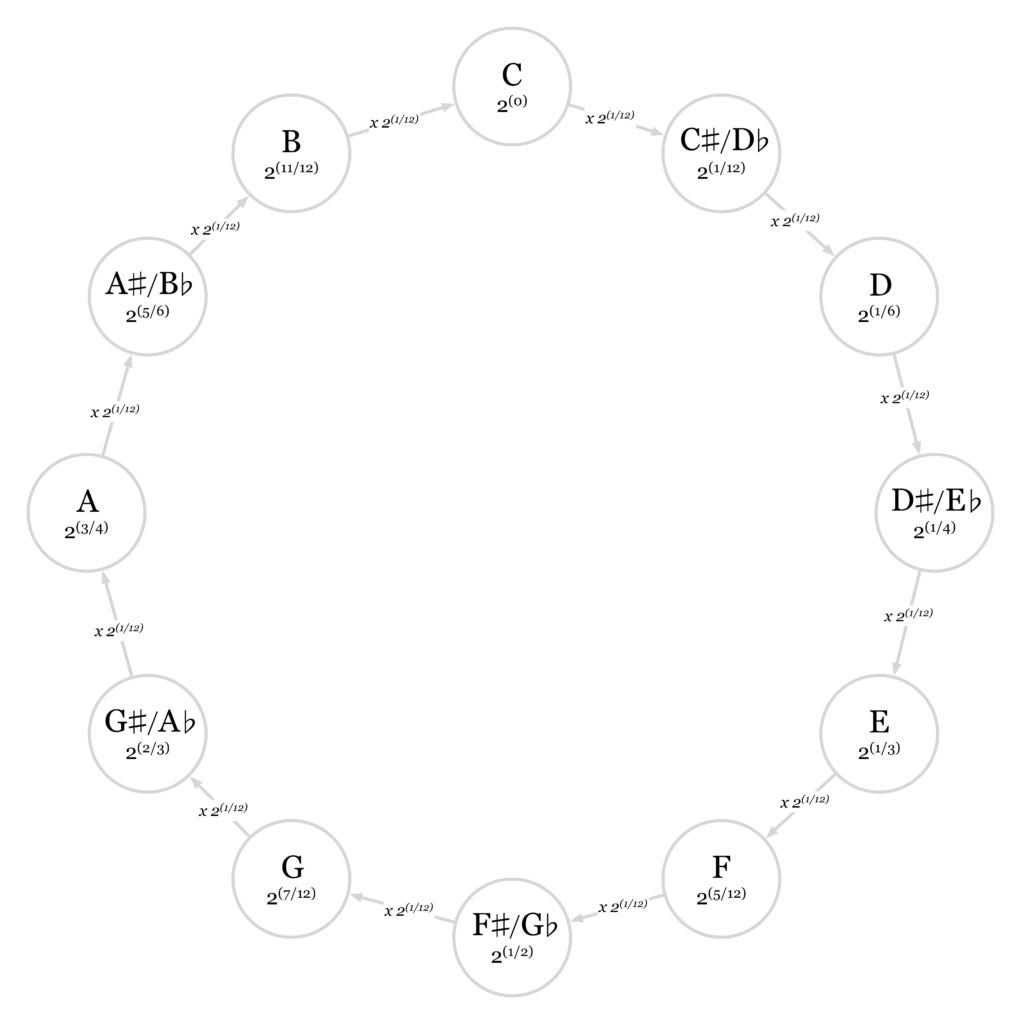
All the conflicts from five-limit get resolved by brute force in 12-TET. There is only one D, at 2(1/6) Hz. There is only one A, at 2(3/4) Hz. The problem with endlessly ramifying enharmonics is solved too; they are all regularized out of existence. B-sharp and C are identical at 1 Hz. C-sharp and D-flat are identical at 2(1/12) Hz. D-sharp and E-flat are identical at 2(1/4) Hz. E-sharp is the same as F at 2(5/12) Hz. And so on. Unlike the near-circle of three-limit (really an infinite spiral), in 12-TET the circle of fifths is an actual closed circle.
The benefit of 12-TET is that it's nice and simple. The bad news is that no intervals are really in tune except octaves. Some of them are close. The 12-TET G at 2(7/12) Hz is almost indistinguishable from G at 3/2 Hz. However, the 12-TET E at 2(1/3) Hz is noticeably sharper than E at 5/4 Hz. Like three-limit just intonation, 12-TET gives you great-sounding fifths, but not-so-great-sounding thirds. Maybe this is why modern musicians like power chords so much.
Western European music is reasonably well suited to 12-TET, but the blues is not. You need finer pitch gradations than the piano-key notes can give you. This is why blues and jazz musicians prefer instruments with fine pitch control, like trumpet, trombone, violin, and the voice. This is also why blues guitarists bend strings "out of tune" and use slide: they are looking for those in-tune notes between the frets.
As with any discussion of this material, the big question is always: who cares? Music theory is confusing enough, why even bother engaging with a historical tuning system that no one even uses anymore? My motivation for wanting to learn all of this is that I like things to make sense. You don't need to understand all the nuances of historical tuning systems, but it is good to know they exist. Think of it like English grammar, which seems insane and nonsensical until you find out that it's an awkward hybrid of Latinate and Germanic languages, the result of French invaders colonizing England. So it is with music theory. Why are music theory teachers so persnickety about writing B-sharp instead of C in the key of C-sharp minor, when it makes no difference at all in how things sound? Now that I know that B-sharp and C used to be totally different notes, I'm more at peace with the spelling convention. Just intonation may be arcane, but at least it makes all the 12-TET arcana more logical and explicable.


